SparseLoco: Scaling Up Top-K Error Feedback with Local Optimizers for LLM training
Today, the Templar team is excited to announce SparseLoco (Sparse Aggregation DiLoCo) — an optimizer that improves communication efficiency in distributed LLM training. SparseLoco combines benefits of local multi-iteration methods (e.g., FedOpt, DiLoCo) with gradient compression methods (DeMo, top-k error feedback, etc).
The Communication Bottleneck
A key challenge in training large language models over the internet is the communication cost between nodes. Nodes in a distributed training system typically communicate pseudo-gradients which are aggregated to make updates. Naively, these can be the size of the model which is not scalable for internet connectivity.
Error-feedback (EF) based gradient compression (Seide et al, Stitch et al) is a classic family of approaches for reducing the communication cost in distributed training. Templar currently utilizes an error-feedback gradient compression method DeMo (Peng et al) which has demonstrated the ability to reduce the communication cost of pseudo-gradients in LLM training by up to 500x (including quantization) compared to standard DDP without quantization. This method was used to train Templar’s first 1B permissionless mode (Lidin et al) . However, gradient compression alone has limitations. Individual nodes can only process a limited amount of data before requiring synchronization. Even with compressed payloads, communication overhead often matches compute time, and processing more data in these schemes typically hits diminishing returns.
To address the high frequency of synchronization, multi-iteration methods like DiLoCo propose an alternative. Instead of synchronizing after every batch, each node performs multiple local optimization steps on its own data, accumulating changes locally before communicating a summary of the updates. This paradigm is naturally complementary to gradient compression, and the concept of combining local steps with quantization and sparsification has been explored previously for CNNs (e.g., Basu et al) and for LLMs without error feedback in (Douillard et al 2025). However, how to combine error feedback with multi-iteration approaches has not been studied in detail for LLM training. By combining both approaches, we achieve the best of both worlds: synchronizing infrequently due to the local steps, and communicating compactly at each synchronization point due to gradient compression. There are several possibilities for how to combine these ideas which we have explored.
Our key findings are as follows:
In order for top-k methods to work with DiLoCo we need to remove the momentum of the DiLoCo outer optimizer and apply error feedback and compression directly on the DiLoCo pseudo-gradient
In the DiLoCo setting the approach of DeMo in applying the DCT actually harms performance while Chunking and Top-k compression gives the best performance
SparseLoco is able to improve over both DiLoco in DeMo in loss despite communication much less
Our Proposed method is summarized in the algorithm block below
The compression function found on line 11, C(.) , can often take many forms in the literature including top-k and random-k compression, quantization, and low-rank decomposition. These have also been used in combination (Wang et al).
Experimental results
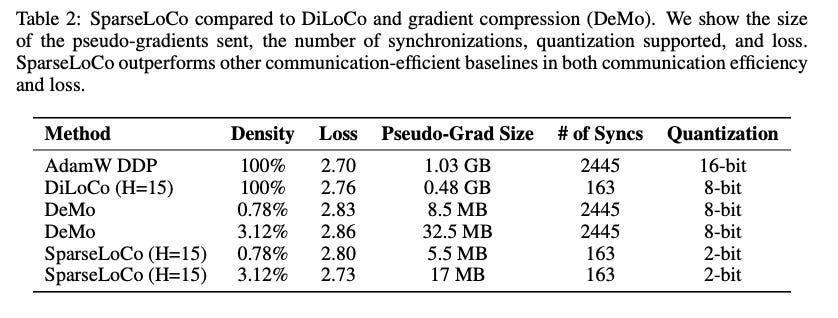
We conduct experiments using a 1B model with a 10B budget. The table below shows the results of our experiments with variants of the algorithm. We use H=15 in these experiments, with 8 workers, a sequence length of 2048, and an inner optimizer batch size of 256 samples per worker. For the compression ratio of top-k, we keep only 0.8% of values as in the DeMo for all cases (SparseLoco, DeMo, and ablation variants). Furthermore, we confirm that results are maintained when 8-bit compression is used.
We first show a summary of the results compared to DiLoco and DeMo.We see that SparseLoco gives a significant advantage in communication efficiency over both popular methods and actually achieves a slightly better loss. We also include estimates for the communication cost of another recent EF-based optimizer (Dion), although code for the method is currently not available.
Notably, SparseLoco achieves a gradient communication reduction of 50x compared to 8bit quantized DiLoCo (Jaghour et al). Compared to Demo, SparseLoco is able to usefully process 15x or more data thus giving significant advantages to both.
We now dive into some of the key design decisions for SparseLoco
Outer momentum conflicts with error-feedback
Our initial attempts to naively combine DiLoCo outer loop with EF gradient compression yielded poor results. We hypothesized the reason for this is the tension between the momentum used in DiLoCo and the error feedback term utilized in compression, with the DiLoCo outer optimizer momentum essentially reinforcing residual error and making it difficult to correct error. We found that simply setting outer momentum=0 (in other words outer optimizer to SGD) yields much better performance. We observed that due to the significant compression the error feedback can serve a similar purpose to DiLoCo’s outer optimizer state. Note that we did attempt to tune the outer momentum but only very low values avoided performance loss while not beating just using SGD.
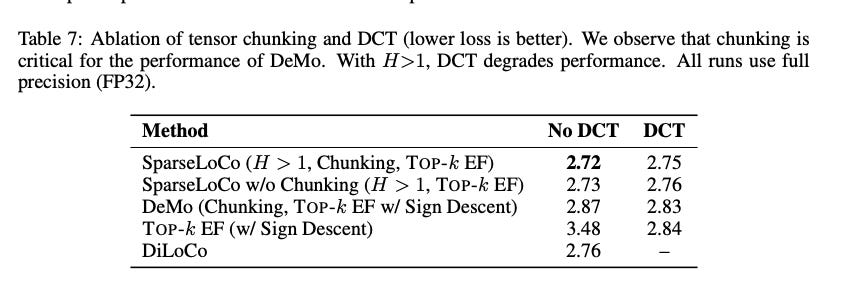
Ablating DCT and Chunking
Classically top-k operation is applied on the entire set of model parameters or at the tensor level. Here we considered several possibilities for the Compression function:
Tensor Top-k - We apply the top-k operation on each tensor taking only the top % of highest values
Chunked Top-k - A fixed size chunk (e.g. 64x64) is defined and all Transformer weight tensors are partitioned into these chunks. The top-k values (as a percentage) are then taken for each chunk. Chunking also requires less communication payload than tensor (or model level) top-k because typically one must transmit both the indices and values, with chunking the number of indices is limited and thus for example for 64x64 sized chunks the indices can be stored as int8.
Top-K on DCT - A 2-D DCT transform is applied on the tensor or chunks before top-k is applied. When H=1 and chunking is used this reduces to the DeMo method
A key innovation in the DeMo optimizer is the use of the DCT transform before top-k compression. However, its role in the compression and interplay with chunking is not well understood. Thus we undertook some ablations to gain insight. The main results are shown in the Table below. We observe based on our ablations in the table below that DCT is quite helpful when applying top-k on the whole tensor (as seen by the poor performance of naive Topk-EF), however when chunking is used the benefits are diminished, putting into question the utility of DCT (which also comes with computational cost). For SparseLoco we observed that DCT can actually harm performance, while chunking improves performance significantly.
A known issue in top-k methods are mismatched scaling between components sent from different workers. We hypothesize that chunking helps to address this issue by reducing the dependence on outlier values and also reduces influence of individual rows or columns in the transformer weight matrix.
We investigated the number of inner steps H, and observed that SparseLoco can maintain performance comparable to Diloco baseline up to at least H=30 inner steps, while the version with DCT began to degrade at H=15.
Conclusion
SpaseLoco represents a step forward in decentralized AI training, enabling nodes to process more data between synchronizations while maintaining high compression. This brings us closer to scalable, permissionless AI training networks.
The key innovations — removing outer momentum conflicts, chunked compression, and strategic DCT application — demonstrate how thoughtful algorithm design can overcome fundamental bottlenecks in distributed training. As we continue scaling toward larger models, these communication efficiencies become critical for maintaining training feasibility across decentralized networks.
Implementation: SparseLoco is now deployed in Templar's production training runs
https://github.com/tplr-ai/templar
Standalone example: code is available
https://github.com/tplr-ai/SparseLoco
Reach out: for technical inquiries please reach out to contact@tplr.ai
Note: An earlier version of this article used the name CCLoco which was changed to SparseLoco along with updated results based on more detailed experiments
References
Basu, D., et al. (2019). Qsparse-local-SGD: Distributed SGD with quantization, sparsification and local computations. Advances in Neural Information Processing Systems, 32.
Douillard, A., et al. (2023). DiLoCo: Distributed low-communication training of language models. arXiv preprint arXiv:2311.08105.
Douillard, A., et al. (2025). Streaming DiLoCo with overlapping communication: Towards a distributed free lunch. arXiv preprint arXiv:2501.18512.
Jaghouar, S., et al. (2024). INTELLECT-1 Technical Report. arXiv preprint arXiv:2412.01152.
Lidin, J., et al. (2025). Incentivizing permissionless distributed learning of LLMs. arXiv preprint arXiv:2505.21684.
Peng, B., Quesnelle, J., & Kingma, D. P. (2024). Decoupled Momentum Optimization. arXiv preprint arXiv:2411.19870.
Seide, Frank, et al. "1-bit stochastic gradient descent and its application to data-parallel distributed training of speech DNNs." Interspeech. Vol. 2014. 2014.
Stich, S. U., Cordonnier, J.-B., & Jaggi, M. (2018). Sparsified SGD with memory. Advances in Neural Information Processing Systems.
Wang, Jue, et al. "Cocktailsgd: Fine-tuning foundation models over 500mbps networks." International Conference on Machine Learning. PMLR, 2023.